Simple DL Part 4: Losses
January, 2021
TLDR
- Loss functions are how we tell the model what information to emphasize or to throw away.
- When thinking about losses, we care about three things: what the model produces, what we are comparing against, and how we do the comparison.
- Losses can be placed on any embedding -- they do not just have to be at the end. The closer a loss is to an embedding, the more influence it will have.
Thinking about Losses
A deep neural network takes in some piece of data represented as an embedding (i.e. a list of numbers). It passes the data through a stack of transformations, each of which produces an intermediate embedding. And then the model outputs some final embedding, depending on what the task is.

It's embeddings all the way down. Also, I like turtles.
During training, we want to quantify how good that final output is. We do this with a loss function. In technical terms, a loss function is a function f(x) or f(x, y) that measures how well the model output x matches a specific piece of information, possibly defined by some external source y. When thinking about a whole training set, the loss function is a measure of how well a model output matches some external distribution.
In practice, the loss function takes the output of the DNN and produces a single number. The DNN tries to minimize that number. We're not gonna dive into how the model minimizes the loss, because I think in practice it's rarely relevant for understanding DNNs. But if you're interested take a look at the wiki page for backprop.
I think of loss functions the same way I think of everything else in deep learning: through the lens of embeddings. Loss functions are applied to embeddings. We take take an embedding from a model that carries some information, and check to see how well it matches the information in an external embedding. During training, the model is trying to minimize the loss. It minimizes the loss by making sure the information needed to construct the final layer is present in the second to last layer. And by making sure the information needed to construct the second to last layer is present in the third to last layer. And so on, all the way to the input features.
I kinda think of a loss function as having some kind of gravitational pull that extracts information, like a magnet pulling out gold from a heap of trash. Different losses extract different kinds of information from the noise, so with the right combination of losses (and the right inputs) you can solve a huge range of problems.
Making a loss function
To a first approximation, we can tune our model by thinking about how the data is correlated with the outcomes we want, and adding losses that emphasize that data. When creating a loss function, we need to consider three things: the model output, the thing we're comparing against, and the method of doing the comparison. In the simplest case, where we're trying to learn some really basic data distribution y = f(x), our loss function is really simple. For a given datapoint x, we look at the model output f(x), compare it against the ground truth value y, and calculate the loss as L = |y - f(x)|. The model is trying to minimize the loss, so over time f(x) will match y.
Why do we use an absolute value in our loss? Because if we don't, the model will minimize the loss by making f(x) really really large, thereby making the loss (infinitely) negative. Remember, models cheat.
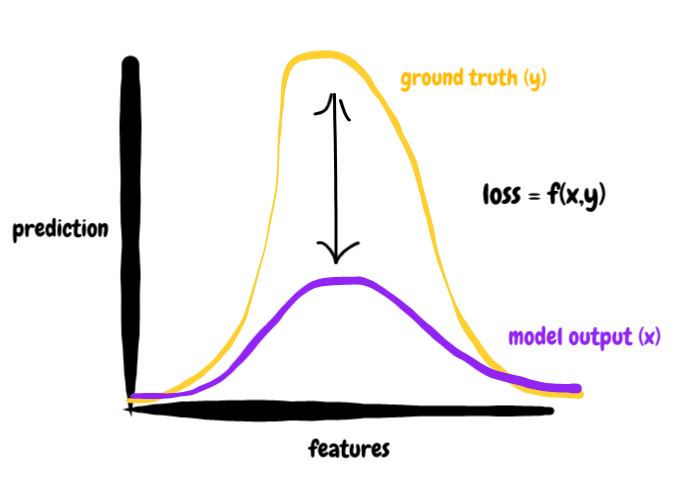
For most tasks, the loss is defined as some kind of distance between two distributions -- the model output and some external truth distribution -- that quantifies the model's performance. In this case, the distribution is pretty straightforward because we're dealing with only two dimensions. But we can do the same with much higher dimensional data, say a 64d embedding.
So how do we change a loss function?
It's hard to figure out exactly how changing the loss will impact the model -- I mean, we can calculate the outcomes with math but realistically that does not provide us with a great understanding of how the model will respond, because of the whole cheating model thing. As a result, changing the losses of a model can be pretty volatile.
One real world application that helped this all click for me was thinking about problems where you have a really skewed distribution of data. In Part 3 we talked about how it's important to make sure there are no hidden correlations in your data. But sometimes you don't have any other choice. Most medical/health problems run into this issue -- most of your data is from people who don't have the disease. For some rarer diseases, you might have a healthy/unhealthy data ratio of 1:1000. Which, on its own, will basically just result in the model returning a 'healthy' verdict for every single input. Not exactly that useful.
Let's say we're working with COVID patients. We can't get more COVID data. We CAN oversample the infected patients in our dataset to try and balance things out. And then there's a third route: we manipulate the loss.
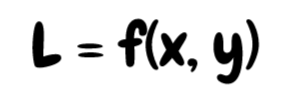
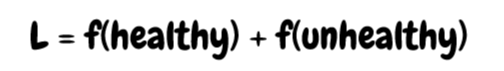
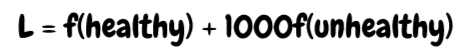
In short: every time the model sees an infected patient, we multiply the loss by 1000x. In other words, the model will 'care' about the unhealthy patients 1000 times more than the healthy ones. Mathematically, this is because the loss is now much more impacted by the unhealthy patients.
Since there are way more healthy patients than unhealthy ones, it all (ideally) balances out. But we can actually start being clever about this. In a lot of medical applications, we care a lot about false positives or false negatives, but rarely both. For an uninvasive COVID screen, we want to make sure we don't accidentally let people who are infected through even if it means getting some false positives. So, we increase the penalty for missing infected patients, making the model more likely to flag all the infected. On the flip side, for a more invasive surgical procedure, we definitely want to make sure that the model is really sure that a patient has COVID. So, we increase the penalty of misdiagnosing healthy patients, making the model less likely to send a healthy person to surgery.
Instead of perfectly balancing the loss function, we can bias the model by weighting one label higher than the other. More generally, for any model, we can increase the weight of specific parameters in the loss to produce specific outcomes (or by adding more terms to the loss).
Losses on other parts of the model
So far, everything in this post has been about losses on the output of the model. But the loss can be anywhere. A loss is a way of converting two embeddings into a single value that can be minimized. Since the model is just a stack of embeddings, you can put a loss on any part of the model. Fitting with the 'gravitational pull' model of loss functions, the closer a loss is to an embedding layer, the more impact the loss will have on that layer.
To use a real world medical example, let's say we had a model that was trying to predict whether or not a patient had diabetic retinopathy given an image of a retina. We could build a simple classifier, but we may be throwing away a lot of useful labeled data like measuring the amount of new veins in the eye or the presence of fluid in the retina (both symptoms of diabetic retinopathy). To make sure our embeddings contain the right information, we can add these additional symptoms to our loss function with multiple model outputs.
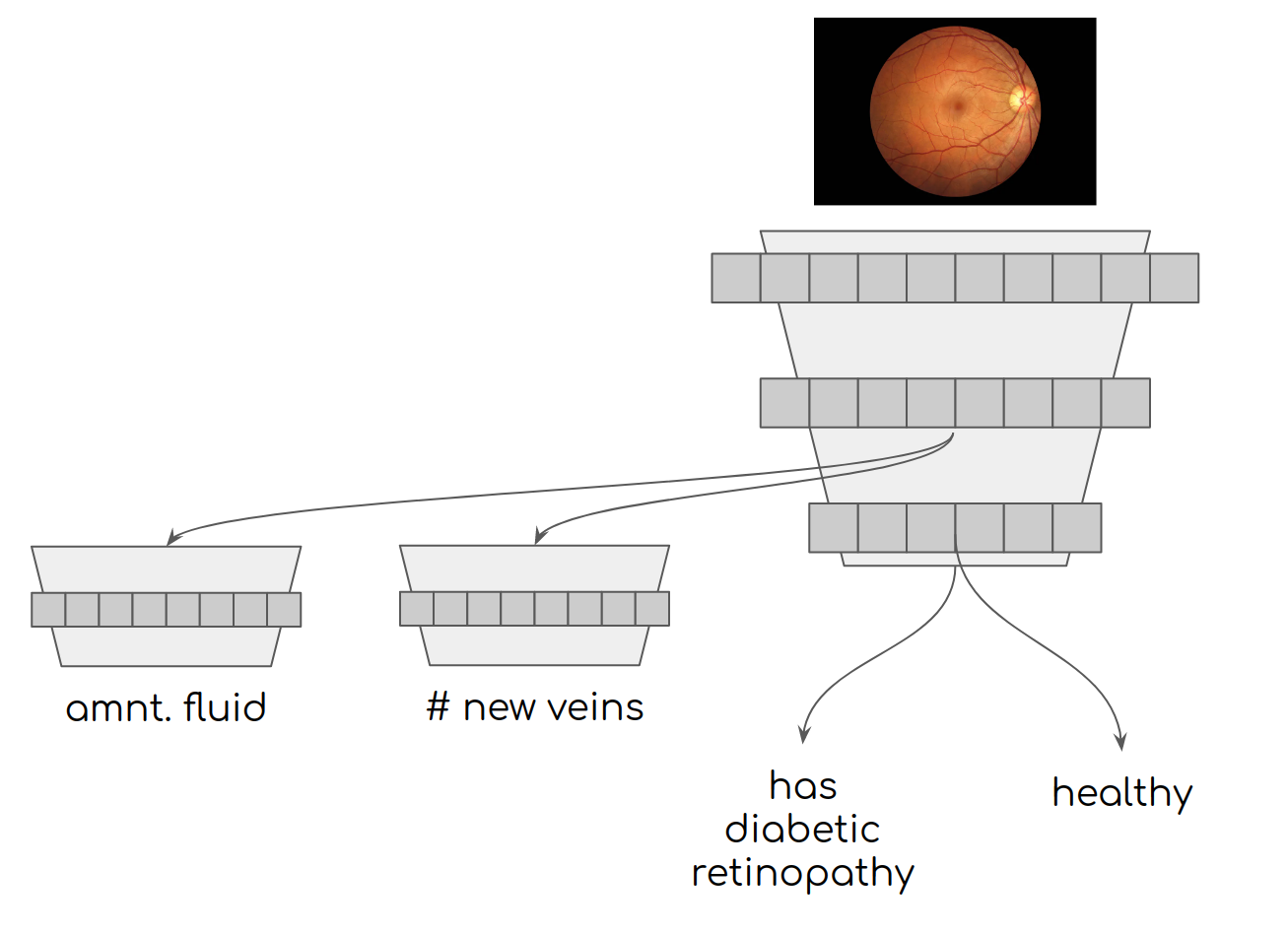
Adding symptom information as multihead losses so the underlying embeddings capture more useful information.
I've kinda been pretending that losses on other model layers are rare, but actually, they're really common. Just about every deep learning model uses some kind of regularization loss (for example, l2 loss) to prevent the weights from growing too large. The ability to add arbitrary losses on different layers is also what powers a ton of unique deep learning models, including: multi-modal inputs/outputs, distillation, GANs, and more.
Conclusions
Loss functions are hard to understand, because changing them doesn't always do what you expect in the model. But they are also super important, because without the loss we have no way to actually control what the model is doing. It's like doing surgery with a hammer. Messy. And it's rarely the right answer, if you have a working model that you're trying to improve.
But if you have a model that doesn't work at all, change the loss. Change it with abandon, because your current loss isn't right at all.