Simple DL Part 5: Canonical Tasks
March, 2021
TLDR
- A canonical task defines how a model learns.
- There are three canonical tasks: classification, multiclassification, and regression.
- Each canonical task has a canonical loss: softmax cross entropy, sigmoid cross entropy, and mean squared log error, respectively.
What is a Canonical Task?
There is a lot of chaos in deep learning literature. Every year, it seems like hundreds of models are published, each with dozens of possible applications. It can be tough to figure out what a model actually does and how it can be used.
Over time, I developed the idea of a Canonical Task to help me get through the noise. For me, a Canonical Task is some sort of indivisible thing that defines a models purpose. Depending on what's more intuitive, you can define these tasks based on what the model produces, or based on how the model learns. It turns out that even though there are so many different models, there are only three canonical tasks. These are:
- Classification
- Multi-Classification
- Regression
Every deep learning model in the whole world can be broken down into these three tasks. And each of these tasks comes with a set of 'default' loss functions too. So if you have a never-before-solved problem, the first thing to do is figure out which task your problem falls under, and then pick a corresponding loss, and you've already solved half the issue in front of you.
Let's talk about what each of these Canonical Tasks mean in a bit more detail.
Classification
A classification task is when you train a model to predict whether an input is one of a set of mutually exclusive things. Imagine we want to train a pet classifier. We want to pass the model some input, maybe an image. On the output, the model needs to decide whether the input represented a dog, a cat, or a fish. The model cannot say the input was a dog AND a cat AND a fish -- these are mutually exclusive categories. If the model is more confident that the input is a cat, it has to be less confident that the input is a dog or a fish.

An ML model learning a classification task.
What kind of loss would we use for classification? Well, as we said in Part 4, we care about three things: what the model produces, what we are comparing against, and how we do the comparison.
Going back to our pet example, we want the model to produce a prediction for three categories. And, these three categories are totally unrelated from each other, except that they are mutually exclusive. How do we actually represent abstract concepts in a model? Well, a model only has one building block -- the embedding. Remember, a model is just a stack of embeddings. So we basically have to enforce an external constraint on the last embedding of a model, and call that the output. This gives us a lot of flexibility -- we can say that the model outputs a vector of size three (or an embedding layer of size three), and as long as we are consistent we can arbitrarily assign each spot in the vector to an animal. So, spot 0 is 'dog', spot 1 is 'cat', spot 2 is 'fish'. If the model puts a really high value in spot 0, it's predicting dog.
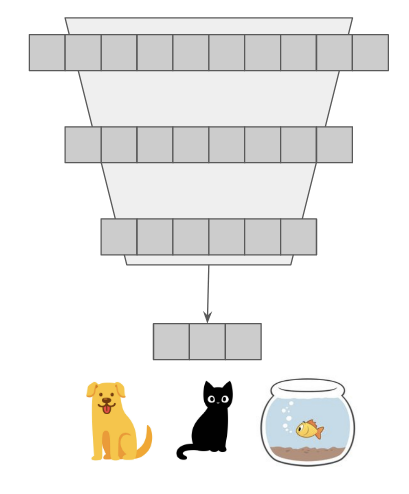
A categorical pet classifier. Each spot in the output vector is associated with a speific animal. Homework question 1: one possible design is for the model to output a numeric value from 0 to 2, and then have if statements that threshold (e.g. if 0 < x < 1, assume the model is predicting dog). Why is this a bad approach?
One problem. Right now, there's nothing stopping the model from putting super high weights on more than one value! What if the model outputs something like [1, 1, 1] -- it thinks the input image is a dog and a cat and a fish. Since we know our inputs are mutually exclusive, we need to force the model to behave by constraining the inputs relative to each other. Softmax to the rescue. The softmax function takes in an input vector and reweights it so that the total value of all of the parts of the vector sum to one. Since we constrain the sum, the model has to make a choice -- if it puts more weight on one part of the vector, it has to put less weight on other parts of the vector. And, because it sums to 1, we can think of the output of the softmax as a probability distribution.
A softmax also gives us a pretty natural way to represent our ground truth. We can compare the model's outputs against a 'perfect' output. So, if we input a picture of a cat, we expect the model to output something like [0, 1, 0]. Or if we put in a picture of a dog, we want the model to output [1, 0, 0].
Ok, so we know what the model outputs, and what we compare against. How do we do the comparison? We can use something called a cross entropy loss. Explaining cross entropy is kinda out of scope for this piece, and also kinda irrelevant. Think of it as a black box that measures the difference between two probability distributions. Basically, it will look at the model's output, and look at the ground truth, and calculate a difference between them that the model can minimize. Take a look at the wiki page for more.
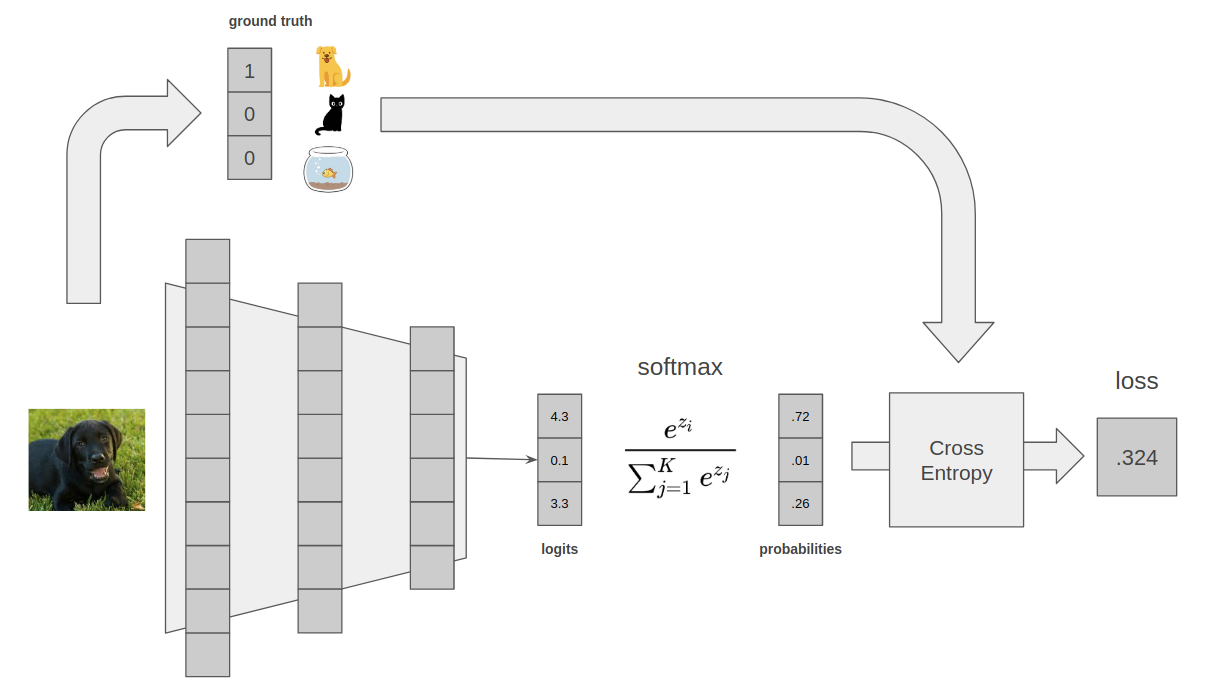
An end to end classification example, where the model is 72% confident that the input image is a dog. For intuition purposes, it is much more important to understand what each building block is doing, than it is to really understand the numeric values. For example, I personally don't really care that the loss is .324, I only care that the loss is being minimized in a way that makes sense over many steps.
This setup is so common for classification tasks that it's basically the default. Every stats package worth its salt has a function called softmax cross entropy, that calculates the loss above.
Multi-Classification
A multi-classification task is really similar to a classification task, except this time the possible outputs are not mutually exclusive. Maybe we have a dataset of zoo animals, and so it's possible for an image to contain dogs and cats and fish in the same image. We would use a multi-classification model to represent this data.
A pretty common multi-classification loss is sigmoid cross entropy. This loss is similar to the softmax cross entropy, but we use a sigmoid nonlinearity because that is applied per element and simply converts each individual element to a value between 0 and 1. Because the individual elements aren't constrained by each other, multiple elements can be set to 1 (i.e. 'predicted'). One way to think about this model output is to imagine that each individual element is its own predictive function, and any value above a threshold is therefore considered a model prediction.
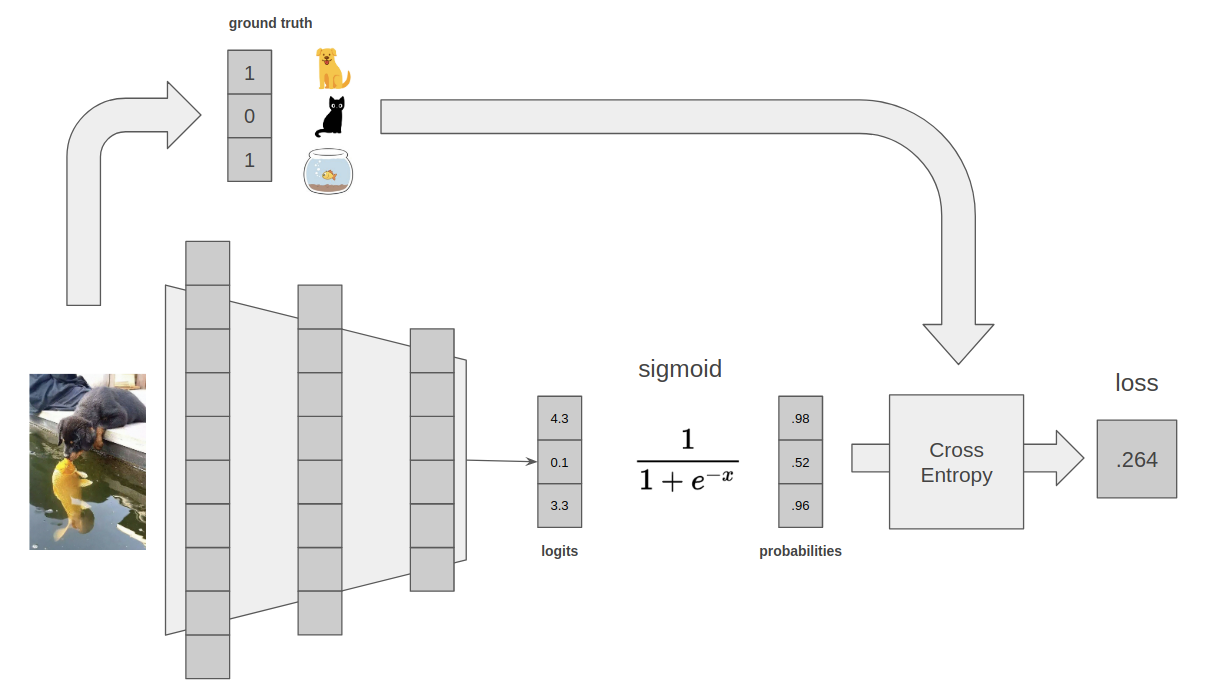
An end to end multi-classification example, where the model is 98% confident that the input image has a dog, and 96% confident the input image has a fish. Note that the sigmoid function calculates a loss per element, so to get the final loss as a single number we need to calculate an average or a sum. Homework question 2: given the above, what might a reasonable threshold be to determine when we consider a model output a 'prediction'?
This setup is also really common! So, as you might expect, every stats package also has a function called sigmoid cross entropy, that calculates the loss above.
Regression
Regression tasks are pretty different from the other two. In classification and multiclassification tasks, you have to bucket your outputs into discrete categories. With regression, you train a model to predict continuous values instead. In other words, regression tasks produce outputs where predicting a higher or lower value matters because there is a numerical relationship between those values. If we wanted to predict housing prices, or case counts for some disease, or some embedding value from a different model, we want to use regression.
There are a bunch of possible losses here, such as difference, mean squared error or mean squared log error. There are theoretical reasons to prefer a log error, but basically as long as you have some measure of distance between the ground truth and the model prediction as your loss, you are probably good.
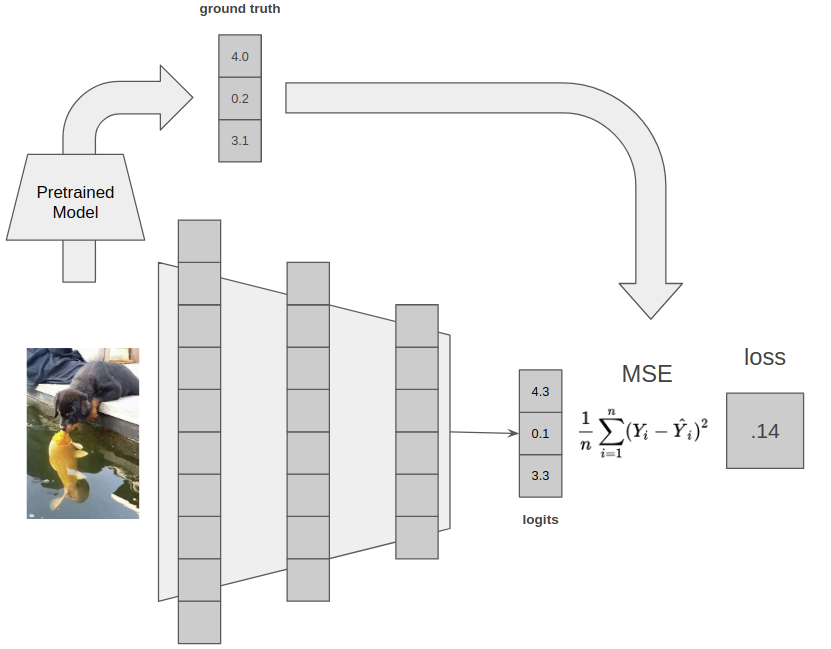
An end to end regression example, where we are training a model to try and predict the outputs of another model. This is really common in ML research. Let's say we have a really big model that is very accurate, but too large to be practical. We can train a smaller model by having the smaller model predict the larger model's embeddings. This is known as 'distillation' in ML terminology, and is a classic regression task.
Outputs vs. Tasks
The tasks above aren't necessarily the same thing as the model output. These tasks basically define ways for us to think about and categorize models (or subsets of models). The actual outputs can be anything within the model. For example, we may want to train a model with a multiclassification loss on images, in order to pull out the top layer of the model as an image embedding. For your own intuition, it's important to avoid confusing these two concepts (even though they are the same for many learning tasks).
Conclusions
Whenever I get stuck with a new ML problem, I always start with canonical tasks. If I can fit my problem into one of the canonical tasks above, I've already solved half the problem. Alternatively, if I have a bunch of data lying around that I know will work for one of the tasks above, I can try to restate the problem such that that data becomes useful in some way. Thinking about ML building blocks like this will inevitably help save a lot of time and frustration. A lot of the SimpleDL series has been focused on intuition, but I think this piece in particular is critical for anyone who is hoping to do ML in practice.
Homework Answers
- A model has no default understanding of categories. We need to enforce that on the model. Otherwise, the model will assume that everything is continuous, and therefore numerically comparable. If we had a model that only output a single value, the model would interpret the categories as having some sort of mathematical relationship -- namely, that a 'fish' is larger than a 'dog'. This doesn't make sense, and would likely result in a bad training scheme.
- It's tempting to say something like 0.5, and just assume that whenever a model predicts above 50% probability it's a 'prediction'. But most real world tasks aren't that simple, and there is a meta level of tuning required to find an appropriate threshold. If we just used 0.5 in the above example, the model would have predicted 'cat' with 52% accuracy. If we set the threshold to something like 0.75, it would only (correctly) predict 'dog' and 'fish'.