Simple DL Part 2a: What are Embeddings?
December, 2020
Embedding Basics
Ok now for the long version. We'll start with a definition: an embedding is a list of numbers (AKA a float vector) that represents some information. You can have embeddings for just about any kind of information out there. There are word embeddings. There are sentence embeddings. There are image embeddings. There are graph embeddings. There are furniture embeddings. Basically, if you can think of a concept, you can represent it as an embedding.
If you're more mathematically minded, the embedding wiki page has a pretty good formal description/definition of embeddings. The core idea is that an embedding is a mapping between some object (or space) X to some object (or space) Y, such that the 'important' structure of X is preserved. For most deep learning applications, we care about embeddings in metric spaces.
Information vs Format
This is already kinda weird. How can we take any concept and represent it as a list of numbers? To really grasp this idea, we need to remember that information is not the format. This is a core principle of information theory and underpins most of modern computer science. Basically, we can take a piece of information and represent it in any format, and the underlying information won't be any different. We might lose information in the conversion process, but that's due to practical limitations of the format.
An example may help nail all this down. Let's say we have a picture of my wonderful dogs, Sparky and Lego.

Dogs!
There is a lot of 'information' in this picture. Can we convert that 'information' to text without losing any of it? We could try describing the image. "Two dogs" captures most of the information. "One small brown dog and one medium-sized gold dog on a slate grey surface" captures even more. We can keep going like this, with ever more complex descriptions -- a picture is worth a thousand words, after all.
Can we do better? "Two dogs" captures a lot of the information, but its just 8 characters. Information has a compression limit; 8ch is simply not enough data storage capacity. It will always leave something out. Instead, lets go pixel by pixel and write out the colors. Starting from the top left, we could write "grey, grey, grey, light grey, light grey, grey, grey...". Not exactly Hemingway, but it would be a perfect representation of the image. We would capture all of the information.
The leap to an embedding is straightforward. Replace our words/colors with RGB values -- something like [(128, 128, 128), (128, 128, 128)...]. Flatten that out, and we've successfully turned our image into a numeric vector that perfectly captures all of original information.
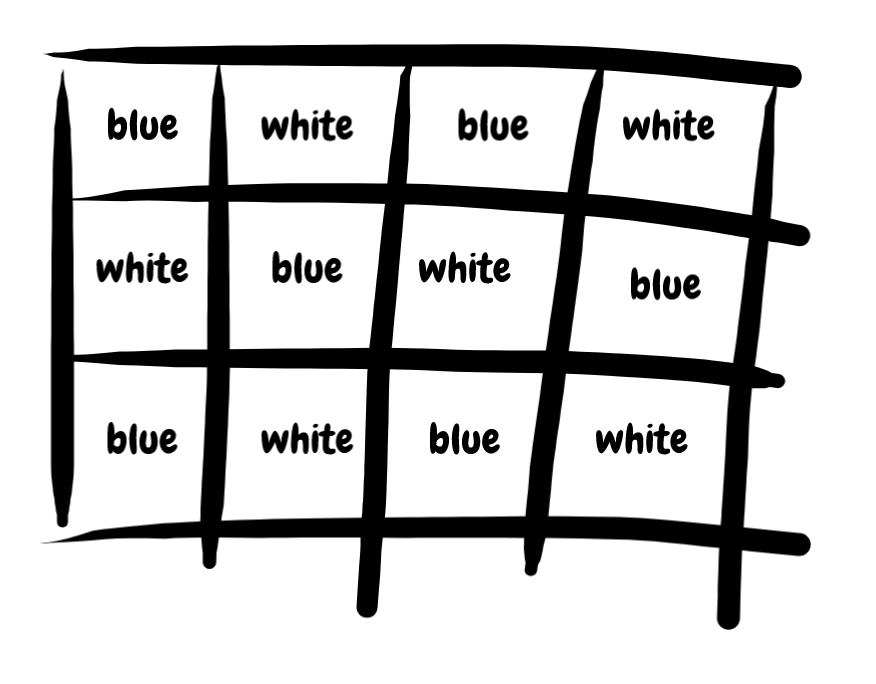
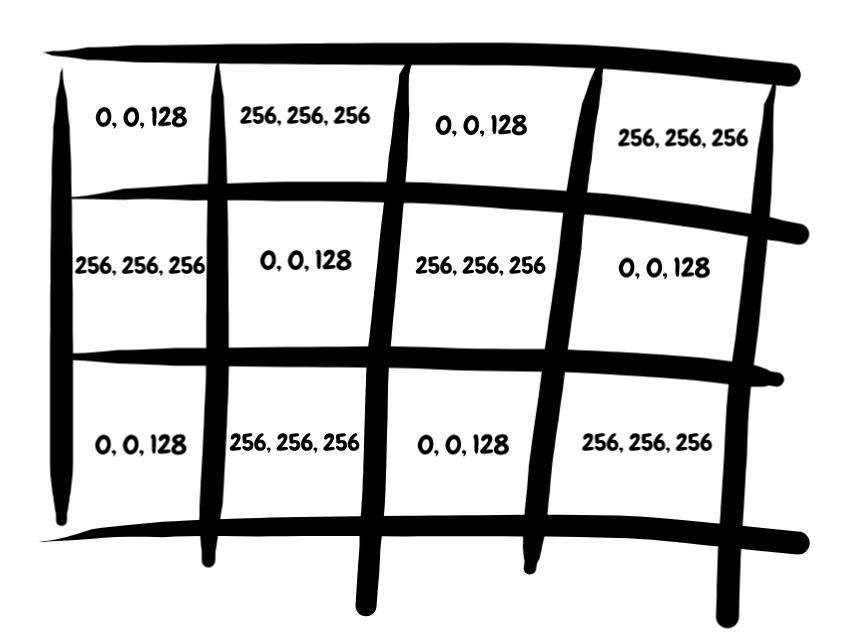
Same information, different formats.
What about text? Can we turn text into an embedding? Well, one strategy could be to turn every character into a unique number, like ASCII. This is why a numeric sequence like 104 101 108 108 111 32 119 111 114 108 100 can be read as 'hello world' by a computer. If we had a really long sequence of text, like a book, we could instead turn every unique word into a unique number. So even though we started with text, we can pretty easily convert to a numeric representation.

Ok so hopefully by now you have some intuition for what an embedding is. Question: is [0.124, 458.2356, 85.3, 2.01] an embedding? Or is it a random list of numbers?
We need to make a small change to our initial definition.
An embedding is a list of numbers (AKA a float vector) that represents some information, as well as a mechanism for encoding and decoding that float vector to something useful. In the examples above, our encoding/decoding scheme was RGB or ASCII. In deep learning, our encoder/decoder is the Deep ML model.
Conclusions
Embeddings are a super unintuitive concept, and I think to really reason about them you have to clear two huge hurdles. Figuring out information vs. format was one of those hurdles -- once I could separate the abstract concept of data from the format it was presented, I began to think in terms of flowing information. And information as a concept is really something that can only live in your head. Data is converted from bits on a disk to pixels on a screen, which is interpreted as lightwaves by our retinas, which is converted electrical signals in our brain...ALL of that is format. The actual information is abstract, existing in a void that cannot ever be actually materialized.
Ok enough poetry.
This section covered how information can be represeneted in a bunch of different formats. In the next section, we'll cover the second big hurdle: how embeddings can be used to convert concepts to computation. We'll talk about why different formats matter, and what we can do with embeddings that make them so powerful for Deep ML.