Simple DL Part 2: Why do we care about Embeddings
December, 2020
Recap
In the previous section, we defined an embedding as a float vector representation of information that, for practical purposes, comes with a mechanism for encoding/decoding the data. We talked about how information was not the format, and how you could perfectly represent information in a bunch of different ways. And we had a few examples of how images and text can be represented as embeddings. In this section, we dive into why embeddings are powerful and key to understanding deep learning.Format Matters
Why do we bother with a float vector in the first place? If we can "perfectly represent information in a bunch of different ways", why lists of numbers? The boring answer is that computers can operate on numbers really easily. The more interesting answer is that different formats let you manipulate your data in different ways.
Float vectors are continuous representations. You can compare them. You can add them together. You can average them. You can do all these neat mathematical operations on them to quickly and efficiently shift your data around. And this is really powerful, because you can turn concepts into computation.
Let's say we wanted to represent two concepts: gender, and royal status. We can represent these as axes on an XY coordinate plane, so that any coordinate [X, Y] corresponds to a gender/royal status pairing.
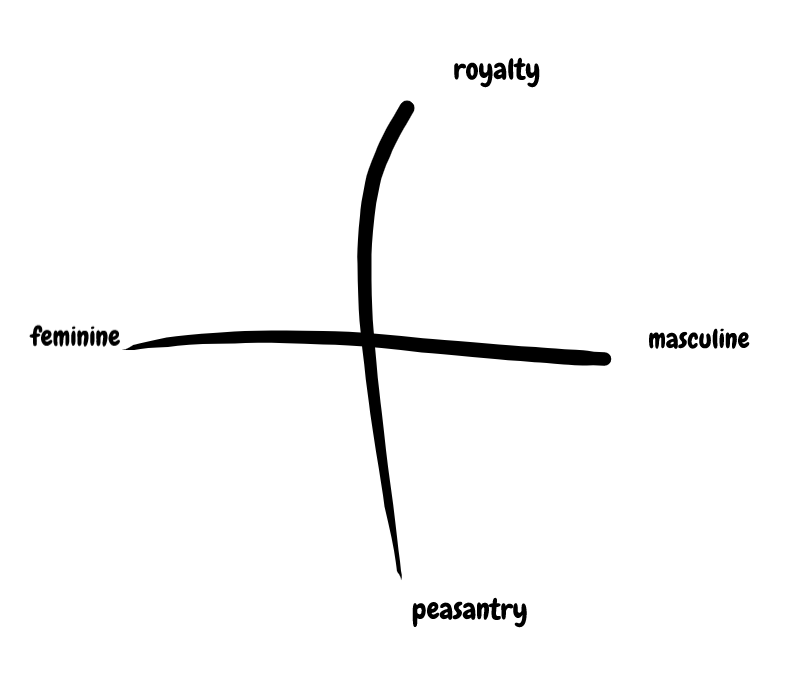
Not a political compass meme.
With this rough coordinate system, we can embed words by mapping them into x-y values. For example, we might say the word King is mapped to coordinates [1, 1]; the word Queen is mapped to [-1, 1]; the word Man is mapped to [1, 0]; and the word Woman is mapped to [-1, 0].
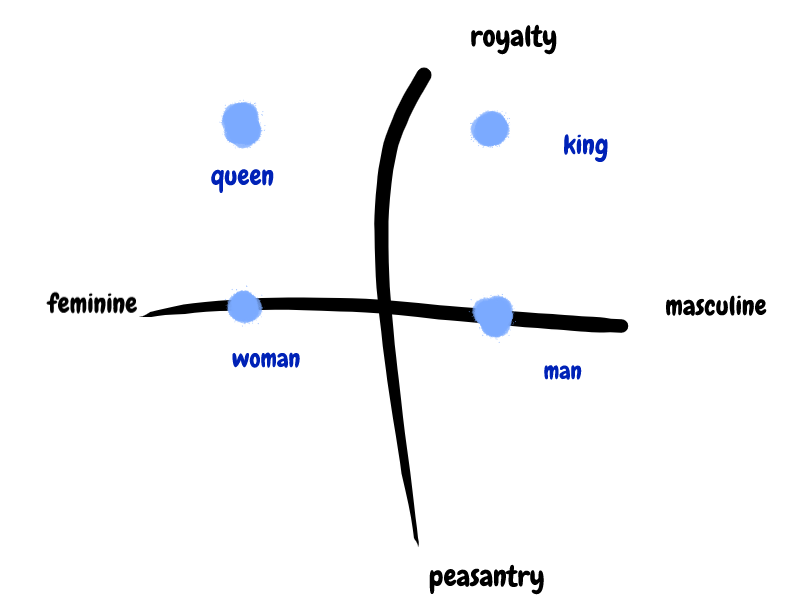
Now we can do some really cool stuff. We could average words together to find other words near their conceptual midpoints. We could subtract words to remove their meaning, or add words together to search for specific related concepts. We could add new dimensions, like a Z-axis for 'Age'. We can quantify words and use math to analyze them. That, to me, is magic.

We can do things like this. This example is pretty famous in NLP, thanks to a word embedding generator called Word2Vec.
We can do all of this magic because float vectors correspond really well to geometry. People aren't great at remembering lots of numbers, but we do a great job with spatial reasoning. Embeddings allow us to turn concepts into points in space, where we can visualize things like 'distance' or 'surfaces'. When I think about creating a model to embed cars, I imagine a fantasy map where different regions represent specific car makes and models. You have a Mercedes town, which is pretty close to BMW-burg , and kinda far from the Bus-ville. If our map does a good job keeping similar things close to each other, we've solved 90% of the deep learning problem.
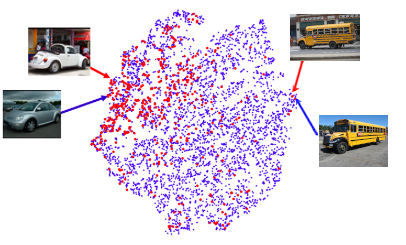
I couldn't get anyone to draw me a fun fantasy map of Car-Land so we'll have to go with the boring technical version.
Imperfect Information
With infinite resources, we could perfectly convert any piece of data from one format to another. That's neat, but also just about useless. Most of the time, we care about removing information, filtering important data from noise. This is especially true in deep learning, where a hotdog image classifier might be taking in thousands of pixel values and returning only a single bit.
Embeddings go hand-in-hand with information compression -- the challenge of a good embedding is to figure out what the important information is. Our map doesn't need to draw every tree and mountain in high resolution detail, but it does need to make sure the borders are in the right spot.
But how do we compress information?
So far we've been isolating the axes of our embedding -- we have a 'gender' dimension, and a 'royalty' dimension, and maybe an 'age' dimension, and they don't mix at all. This makes it easy to draw a map, but the map isn't going to carry a lot of info. To work with larger data, we need to get rid of axes and look at regions. Instead of saying "+Y = royalty", we would say "the area around coordinates [0, 1] is associated with royalty". Notice how we are defining the region with both coordinates. As we walk around our coordinates, we're 'exploring' the feature space. This gives us much more freedom to represent different concepts.

A rough idea of how an embedding might represent many concepts in only two dimensions. The axes aren't relevant anymore -- each point is still an X/Y value, but each semantic meaning has it's own area of the map. Homework question 1: is this a good or bad embedding? Why?
Because we can slice our float vectors all sorts of ways, we can create millions of semantic combinations that a human would never be able to remember or process. Luckily, we don't need to -- neural networks do it for us. When a deep model is training, it's learning how to draw a super high dimensional map at each layer. And, it can mix and match input data in all sorts of arbitrary ways to figure out where the imaginary lines should be, and which concepts should be close to other concepts. Then, during inference, the model reads the map back on some new data point to see what's nearby, and use the map to make decisions.
Features, Embeddings, and Losses: Making a Model
Wait. How does a deep model decide where the imaginary lines should be? What does it mean for concepts to be 'close together'?
Let's take a step back. Every deep learning model is composed of three parts: the features, the embeddings, and the loss function. A "feature" is just a fancy way of saying input data. And the embeddings are the pieces of the model itself -- every deep model is basically just a stack of embeddings.
We'll dive into loss functions in more depth later, but for now think of the loss function as the thing that the model is trying to solve. If you have an image recognition task, for example, the loss will be a measure of how good the model is at recognizing objects in images. During training, the model manipulates the stack of embeddings based on the features and loss.
Each embedding is trying to draw a map based on the information provided by the input features. If we want to identify vehicles, the embedding-map needs to have a clear border between busses and sports cars. If we want to classify text, the embedding-map needs to be able to separate a frown from a smile. And, if a human can't figure out how to draw a reasonable separation boundary for a few data points...well, you probably want to think about your problem and your data some more.
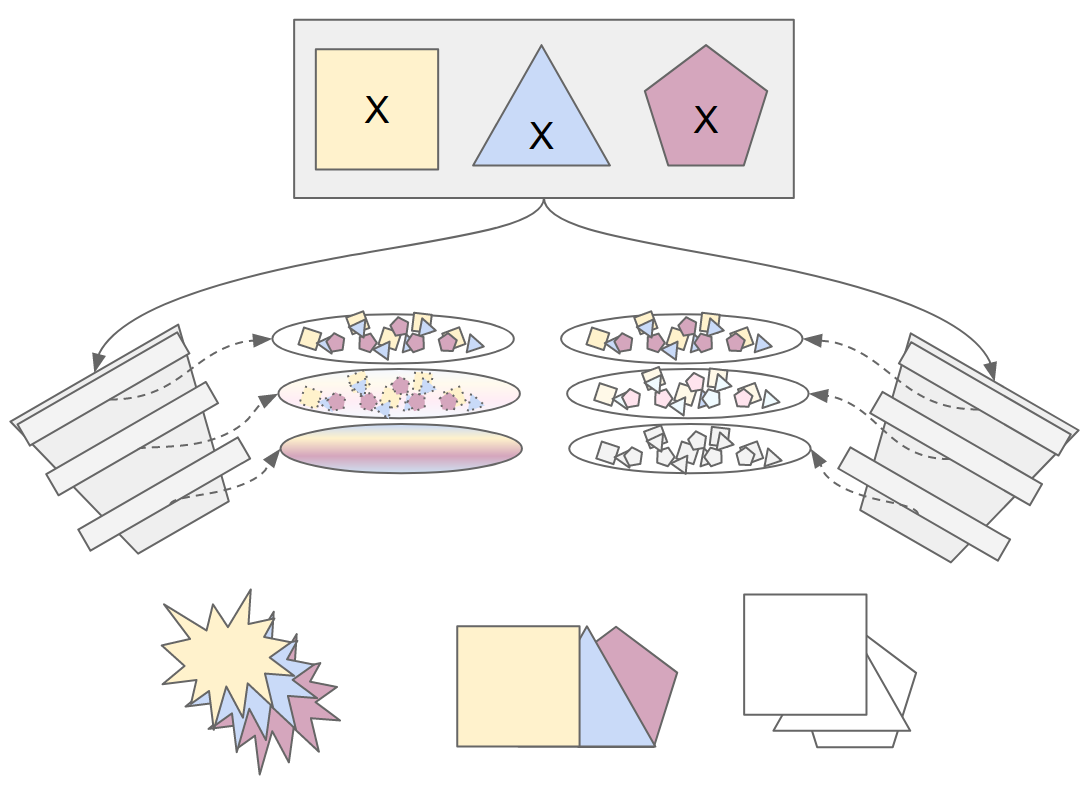
Here, we have two models with the same color/shape feature input. The left model has a loss that is trying to predict color, and the right model has a loss that is trying to predict shape. The embeddings store information based on the loss -- the left model embeddings throw away the shape information and retain color, while the right model embeddings throw away color information and retain shape.
Let's ground this in a specific example. Say I'm the embodiment of $SELF_DRIVING_CAR_COMPANY and I want to create an ML model that identifies NYC taxis, because NYC taxis behave erratically on the road. NYC taxis are bright yellow. So, to improve model outcomes, I could remove all other colors EXCEPT for yellow in my input features; or, I could tweak my loss function to have the model predict color as well as whether or not there is a taxi. Reducing the color input gives the model less data to work with, ensuring that our embeddings will have more of the color information we care about. Adding color to the loss encourages the model to retain color information in the underlying embedding-map.
Overall, the features and the loss function constrain the embeddings. Embeddings can only represent information that is provided in the initial feature set. And the embeddings remove (or emphasize) information based on the loss function. In my head, it's like sculpture -- the features are the clay, the loss is the final vision, and the backpropagating gradients chip away or add to the embeddings so that they are they right shape and size.

Sculpting our embeddings by changing the features or the loss.
I think this gets at why Deep ML models are so powerful. You can throw any features and any loss function into the thing, and the inner embeddings will find a way to connect the inputs and outputs. There's also a corollary to this: your models will only ever be as good as your features and as bad as your loss.
I like this framing because it also gives us some insight in how we can change our models so they do what we want. There are really only three levers: we can add new or more features, to try and give the model more to work with; we can change up the architecture, to try and influence how the underlying embeddings mix and match data; or we can modify the loss(es), to sculpt the underlying information as it flows through the model. Each of these approaches has trade offs. Adding more features will always help the model, but getting new data is really hard. Changing the architecture in a useful way requires a stroke of inspiration or dumb luck. And modifying the loss is highly volatile.
There's one other cool thing about this framing. If we're ever confused about what our model is doing, we can take our model embeddings and plot them in 2D, like an actual map. This will let us see whether similar concepts are appearing close or far away. We'll get into debugging models down the line, but Google 'TSNE plots' if you're curious.
Conclusions
This post was so long it already got split in two, and we're starting to move away from embeddings alone, so I'll leave off here.
There are probably other ways to reason about deep learning, but for me the embedding concept is absolutely critical. When I think about deep models, I need to visualize how information flows through the embeddings I've constructed. Over the rest of the series, we're going to try this visualization process with a bunch of popular architectures -- Convolutions, LSTMs, GANs, Graph Neural Networks, Transformers, and more. And hopefully in the process, you'll get a bit more intuition for how deep learning works.
Homework Answers
- There's no right answer! Some parts of the embedding space display coherent semantic proximity -- for example, dogs, cats, and puppies are all close to each other. But other parts of the space aren't really that reasonable -- why are navigational tools next to politics? In general, the conceptual space is way too complex to represent in two dimensions, so whether or not this is a good embedding depends entirely on the problem you are trying to solve.